[CryptoHack] Diffie-Hellman Starter

#1. Diffie-Hellman Starter 1

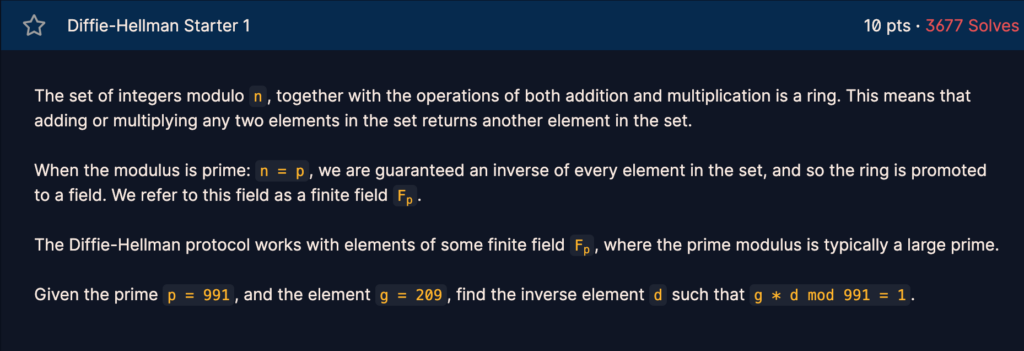
모듈러 n에서 n이 소인수이면 집합의 모든 요소의 역수가 보장되고, 이를 finite field 라고 한다.

diffie-hellman은 이러한 Fp 요소와 함께 작동한다고 한다.

소수로 991, 원소 g=209가 주어졌을 때, mod 991에서 209의 역수를 찾아보자.

이는 유클리드 호제법을 코드로 구현하여 쉽게 구할 수 있다.

def modInverse(a, m):
    m0 = m
    y = 0
    x = 1
    
    if (m == 1):
        return 0
    
    while (a > 1):
        q = a // m
        
        t = m
        
        m = a % m
        a = t
        t = y
        
        y = x - q * y
        x = t
        
    if (x < 0):
        x = x + m0
    
    return x

print(modInverse(209,991))

 

코드 실행 결과는 다음과 같다.

mod 991에서 209의 역원은 569이다.

🚩 569

 

#2. Diffie-Hellman Starter 2

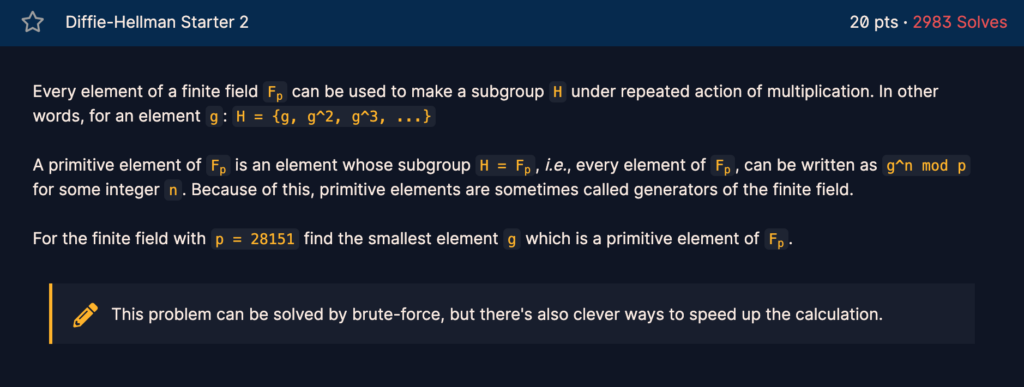
subgroup이 기존 유한체와 동일한 원소들로 구성되어 있다면 이때 subgroup을 생성하는데 쓰인 g는 generator라고도 불린다.

p가 28151일 때, Fp에서 가장 작은 생성자를 찾으라고 한다. 브루트포싱으로도 찾을 수 있는데, 더 효율적인 방법이 존재한다고 한다!

위의 사이트를 보고 효율적인 알고리즘을 코드로 구현해보고 싶었으나 모듈러를 어떻게 설정해야 하는지 모르겠어서 포기했다..

그렇다고 브루트 포싱을 해서 찾는 것은 멋이 없기에 sagemath를 이용했다.

위 사이트를 참고했다.

가장 작은 primitive element는 7이다!

🚩 7

 

#3. Diffie-Hellman Starter 3

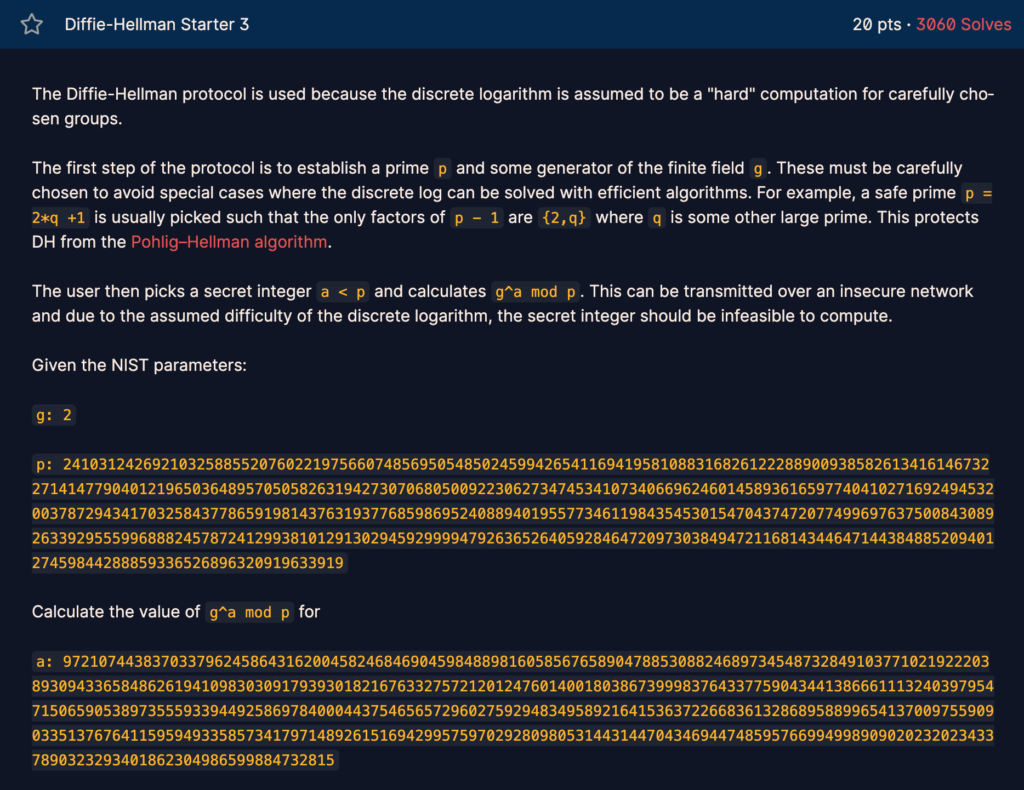
Diffie-Hellman 프로토콜이 쓰이는 이유에 대해 설명해주고 있다. 소수 p와 생성자 g를 안전하게 구하는 방법도 설명해주고 있다. Pohlig-Hellman algorithm은 이산 대수 문제를 풀어내는 알고리즘으로 암호 해독 시간에 배웠던 기억이 있다.

 

우리는 p보다 작은 a를 구해서 g^a mod p를 구하고 이를 상대에게 전송하게 된다. 이렇게 되면 불안전한 네트워크 통신 내에서도 비밀키를 노출하지 않은 채 통신을 할 수 있다.

 

주어진 g와 p, a로 g^a mod p를 계산해보자.

g= 2

p= 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919

a= 972107443837033796245864316200458246846904598488981605856765890478853088246897345487328491037710219222038930943365848626194109830309179393018216763327572120124760140018038673999837643377590434413866611132403979547150659053897355593394492586978400044375465657296027592948349589216415363722668361328689588996541370097559090335137676411595949335857341797148926151694299575970292809805314431447043469447485957669949989090202320234337890323293401862304986599884732815

print(pow(g,a,p))

 

코드 실행결과는 다음과 같다.

🚩 1806857697840726523322586721820911358489420128129248078673933653533930681676181753849411715714173604352323556558783759252661061186320274214883104886050164368129191719707402291577330485499513522368289395359523901406138025022522412429238971591272160519144672389532393673832265070057319485399793101182682177465364396277424717543434017666343807276970864475830391776403957550678362368319776566025118492062196941451265638054400177248572271342548616103967411990437357924

 

 

#4. Diffie-Hellman Starter 4

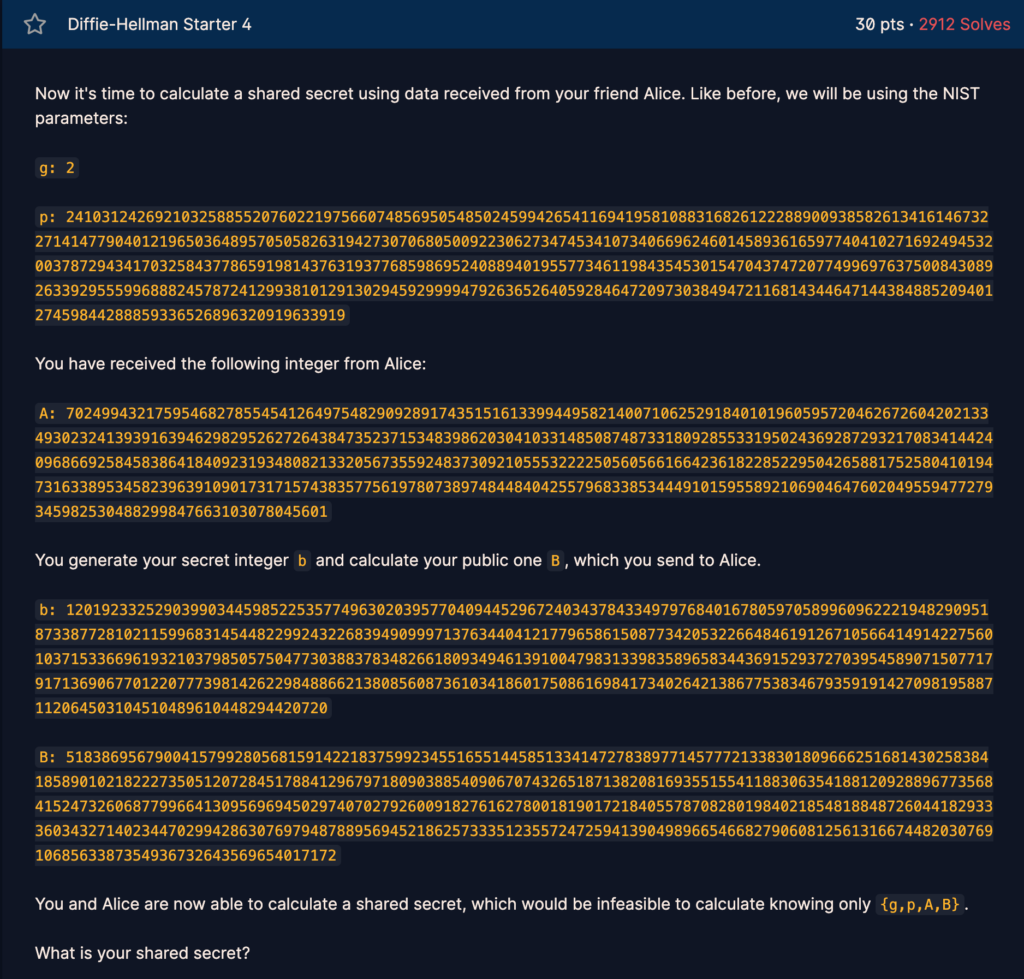
Alice는 Bob에게 g^a mod p를 보내고, Bob은 Alice에게 g^b mod p를 보낸다. 그리고 각각 자신이 받은 것을 보낸 것과 곱해서 g^ab mod p를 공유하게 된다.

위의 문제에서 A를 b 제곱하면 g^ab mod p를 얻을 수 있다.

g= 2

p= 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919

A= 70249943217595468278554541264975482909289174351516133994495821400710625291840101960595720462672604202133493023241393916394629829526272643847352371534839862030410331485087487331809285533195024369287293217083414424096866925845838641840923193480821332056735592483730921055532222505605661664236182285229504265881752580410194731633895345823963910901731715743835775619780738974844840425579683385344491015955892106904647602049559477279345982530488299847663103078045601

b= 12019233252903990344598522535774963020395770409445296724034378433497976840167805970589960962221948290951873387728102115996831454482299243226839490999713763440412177965861508773420532266484619126710566414914227560103715336696193210379850575047730388378348266180934946139100479831339835896583443691529372703954589071507717917136906770122077739814262298488662138085608736103418601750861698417340264213867753834679359191427098195887112064503104510489610448294420720

B= 518386956790041579928056815914221837599234551655144585133414727838977145777213383018096662516814302583841858901021822273505120728451788412967971809038854090670743265187138208169355155411883063541881209288967735684152473260687799664130956969450297407027926009182761627800181901721840557870828019840218548188487260441829333603432714023447029942863076979487889569452186257333512355724725941390498966546682790608125613166744820307691068563387354936732643569654017172

print(pow(A,b,p))

 

코드 실행 결과는 다음과 같다.

🚩 1174130740413820656533832746034841985877302086316388380165984436672307692443711310285014138545204369495478725102882673427892104539120952393788961051992901649694063179853598311473820341215879965343136351436410522850717408445802043003164658348006577408558693502220285700893404674592567626297571222027902631157072143330043118418467094237965591198440803970726604537807146703763571606861448354607502654664700390453794493176794678917352634029713320615865940720837909466

 

#5. Diffie-Hellman Starter 5

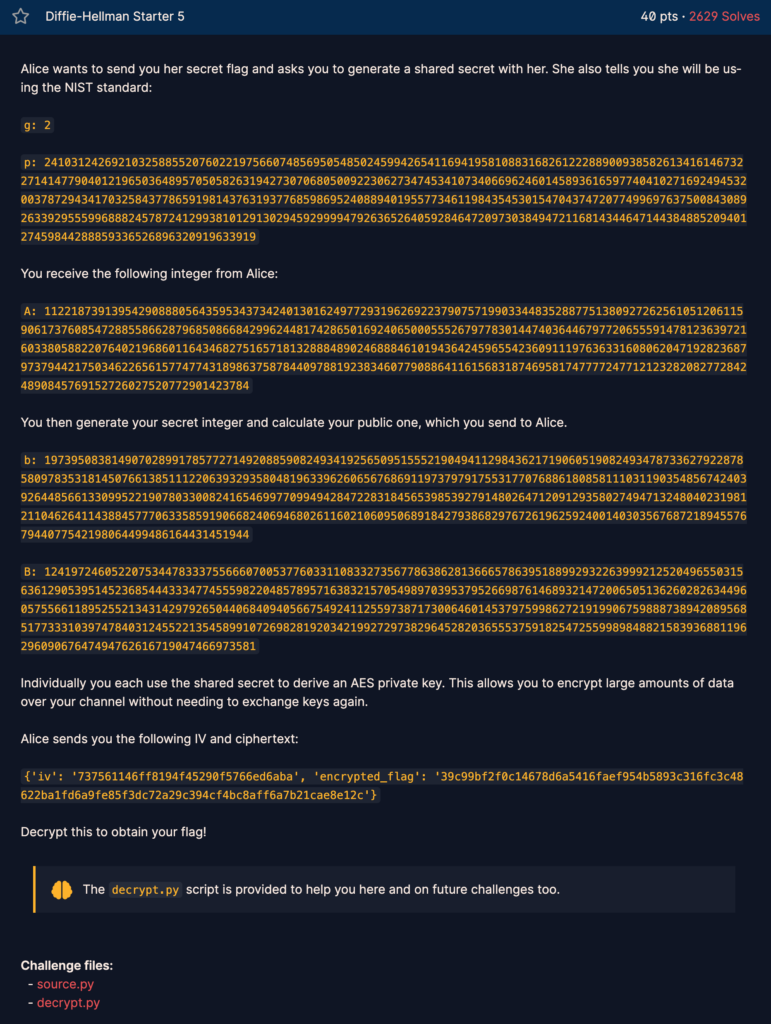
위에서 사용하여 얻어낸 shared secret이 AES 암호화에 쓰인다고 한다. 주어진 파이썬 코드를 보자.

from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import hashlib
import os
from secret import shared_secret

FLAG = b'crypto{????????????????????????????}'


def encrypt_flag(shared_secret: int):
    # Derive AES key from shared secret
    sha1 = hashlib.sha1()
    sha1.update(str(shared_secret).encode('ascii'))
    key = sha1.digest()[:16]
    # Encrypt flag
    iv = os.urandom(16)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    ciphertext = cipher.encrypt(pad(FLAG, 16))
    # Prepare data to send
    data = {}
    data['iv'] = iv.hex()
    data['encrypted_flag'] = ciphertext.hex()
    return data


print(encrypt_flag(shared_secret))

 

먼저 source.py이다. shared_secret을 sha1으로 해시값을 얻어서 ascii로 인코딩하고 앞부분 16byte를 key로 사용한다. iv는 랜덤값을 얻어서 CBC mode로 AES 암호화를 수행한다.

from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import hashlib


def is_pkcs7_padded(message):
    padding = message[-message[-1]:]
    return all(padding[i] == len(padding) for i in range(0, len(padding)))


def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
    # Derive AES key from shared secret
    sha1 = hashlib.sha1()
    sha1.update(str(shared_secret).encode('ascii'))
    key = sha1.digest()[:16]
    # Decrypt flag
    ciphertext = bytes.fromhex(ciphertext)
    iv = bytes.fromhex(iv)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    plaintext = cipher.decrypt(ciphertext)

    if is_pkcs7_padded(plaintext):
        return unpad(plaintext, 16).decode('ascii')
    else:
        return plaintext.decode('ascii')


shared_secret = ?
iv = ?
ciphertext = ?

print(decrypt_flag(shared_secret, iv, ciphertext))

 

주어진 decrypt.py이다. shared_secret과 iv, ciphertext를 바탕으로 이전 encrypt 과정과 비슷하게 decrypt를 수행하고, padding이 있는지 검사하여 있다면 이를 제거하여 평문을 다시 얻어내고 있다.

 

새롭게 주어진 A와 b로 shared_secret을 구했다.

shared_secret = 1547922466740669851136899009270554812141325611574971428561894811681012510829813498961168330963719034921137405736161582760628870855358912091728546731744381382987669929718448423076919613463237884695314172139247244360699127770351428964026451292014069829877638774839374984158095336977179683450837507011404610904412301992397725594661037513152497857482717626617522302677408930050472100106931529654955968569601928777990379536458959945351084885704041496571582522945310187
iv = '737561146ff8194f45290f5766ed6aba'
ciphertext = '39c99bf2f0c14678d6a5416faef954b5893c316fc3c48622ba1fd6a9fe85f3dc72a29c394cf4bc8aff6a7b21cae8e12c'

 

문제에서 주어진 대로 넣어서 코드를 실행해보았다.

flag를 얻어냈다.

🚩 crypto{sh4r1ng_s3cret5_w1th_fr13nd5}